There is increasing evidence that flow and transport processes in soils often cannot be described using classical models that assume uniform flow and transport [e.g., Nkedi-Kizza et al., 1984; Hendrickx and Flury, 2001; Pot et al., 2005; Köhne et al., 2006]. Many laboratory and field experiments have demonstrated the presence of nonequilibrium flow and transport conditions in soils. Nonequilibrium water flow and solute transport in the unsaturated zone can be simulated at present by means of a large number of models of various degrees of complexity and dimensionality. Modeling approaches range from relatively simple analytical solutions for solute transport [e.g., van Genuchten, 1981; Toride et al., 1993] to complex numerical codes [e.g., Šimůnek et al., 2008; Jacques and Šimůnek, 2005]. Numerical models are now increasingly being used since they can be applied more readily to realistic laboratory and field problems as compared to analytical models. The use of numerical models has been further popularized during the last 20 years or so because of the appearance of appropriate software packages in both the public and commercial domains, and the development of increasingly sophisticated graphics-based interfaces that can simplify their use tremendously.

Preferential flow in structured media (both macroporous soils and fractured rocks) can be described using a variety of dual-porosity, dual-permeability, multi-porosity, and/or multi-permeability models [Šimůnek et al., 2003; Šimůnek and van Genuchten, 2008] (Figure below). Dual-porosity and dual-permeability models both assume that the porous medium consists of two interacting regions, one associated with the inter-aggregate, macropore, or fracture system, and one comprising micropores (or intra-aggregate pores) inside soil aggregates or the rock matrix. While dual-porosity models assume that water in the matrix is stagnant, dual-permeability models allow for water flow in the matrix as well. While the uniform flow model and dual-porosity models are available in the standard version of HYDRUS (2D/3D) (Fig. abc), dual-permeability models are not (Fig. d).

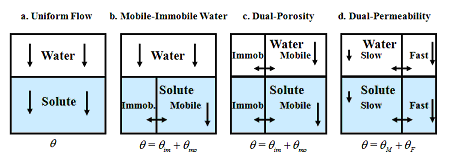
Figure: Conceptual physical nonequilibrium models for water flow and solute transport. In the plots, θ is the water content, θmo and  θim in (b) and (c) are water contents of the mobile and immobile flow regions, respectively; θM and θF in (d) are water contents of the matrix and macropore (fracture) regions, respectively.

Dual-porosity models have long been applied to solute transport studies. Especially popular early on were dual-porosity models in which distinct mobile and immobile flow regions are assumed to be present. Dual-permeability models, in which water can move in both the inter- and intra-aggregate pore regions are now also becoming more popular. Available dual-permeability models differ mainly in how they implement water flow in and between the two pore regions, especially with respect to the degree of simplification and empiricism. Approaches to calculating water flow in macropores or inter-aggregate pores range from those invoking Poiseuille’s equation, the Green and Ampt or Philip infiltration models, the kinematic wave equation, and the Richards equation [Gerke and van Genuchten, 1993a].

We have implemented the dual-permeability module DualPerm (Fig. d) as a supplemental module for HYDRUS (2D/3D) based on the approach suggested by Gerke and van Genuchten [1993a]. The numerical solution of the two-dimensional variably-saturated water flow, and heat and solute movement are described in the HYDRUS (2D/3D) documentation, and will not be repeated here. The DualPerm module is fully supported by the HYDRUS (2D/3D) graphical user interface [Šejna et al., 2018].

The DualPerm module may be used to analyze water and solute movement in unsaturated, partially saturated, or fully saturated porous media. DualPerm can handle flow domains delineated by irregular boundaries. The flow region itself may be composed of nonuniform soils having an arbitrary degree of local anisotropy. Flow and transport can occur in the vertical plane, the horizontal plane, or in a three-dimensional region exhibiting radial symmetry about a vertical axis. The water flow part of the model considers prescribed head and flux boundaries, as well as boundaries controlled by atmospheric conditions.

The governing flow and transport equations are solved numerically using standard Galerkin-type linear finite element schemes. Applications of the DualPerm module are demonstrated on several examples described in the DualPerm manual.

References

Edwards, W. M., R. R., van der Ploeg, and W. Ehlers, A numerical study of the effects of noncapillary-sized pores upon infiltration, Soil Sci. Soc. Am. J., 43, 851-856, 1979.

Gärdenäs, A., J. Šimůnek, N. Jarvis, and M. Th. van Genuchten, Two-dimensional modelling of preferential water flow and pesticide transport from a tile-drained field, J. Hydrology, 329, 647-660, 2006.

Gerke, H. H., and M. Th. van Genuchten, A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media, Water Resour. Res., 29, 305-319, 1993a.

Gerke, H. H., and M. Th. van Genuchten, Evaluation of a first-order water transfer term for variably saturated dual-porosity flow models, Water Resour. Res., 29, 1225-1238, 1993b.

Gerke, H. H., and M. Th. van Genuchten, Macroscopic representation of structural geometry for simulating water and solute movement in dual-porosity media, Adv. Water Resour., 19, 343-357.

Hendrickx, J. M. H., and M. Flury, Uniform and preferential flow, Mechanisms in the vadose zone. In: Conceptual Models of Flow and Transport in the Fractured Vadose zone. National Research Council, National Academy Press, Washington, D.C., pp. 149-187, 2001.

Jacques, D., and J. Šimůnek, User Manual of the Multicomponent Variably-Saturated Flow and Transport Model HP1, Description, Verification and Examples. Version 1.0., SCK•CEN-BLG-998, Waste and Disposal, SCK•CEN, Mol, Belgium, 79 pp., 2005.

Köhne, J. M., S. Köhne, and J. Šimůnek, Multi-process herbicide transport in structured soil columns: Experiment and model analysis, J. Contam. Hydrology, 85, 1-32, 2006.

Mualem, Y., A new model for predicting the hydraulic conductivity of unsaturated porous media, Water Resour. Res., 12, 513-522, 1976.

Nkedi-Kizza, P., J. W. Biggar, H. M. Selim, M. Th. van Genuchten, and P. J. Wierenga, Equivalence of two conceptual models for describing Ion exchange during transport through an aggregated Oxisol, Water Resour. Res., 20(8), 1123-1130, 1984.

Pot, V., J. Šimůnek, P. Benoit, Y. Coquet, A. Yra and M.-J. Martínez-Cordón, Impact of rainfall intensity on the transport of two herbicides in undisturbed grassed filter strip soil cores, J. of Contaminant Hydrology, 81, 63-88, 2005.

Šejna, M., J. Šimůnek, and M. Th. van Genuchten, The HYDRUS Software Package for Simulating Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, User Manual, Version 2.0, PC Progress, Prague, Czech Republic, pp. 280, 2011.

Šimůnek, J., N. J. Jarvis, M. Th. van Genuchten, and A. Gärdenäs, Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone, Journal of Hydrology, 272, 14-35, 2003.

Šimůnek, J., M. Th. van Genuchten, and M. Šejna, Modeling Subsurface Water Flow and Solute Transport with HYDRUS and Related Numerical Software Packages, In: Garcia-Navarro & Playán (eds.), Numerical Modelling of Hydrodynamics for Water Resources, An International Workshop, Centro Politecnico Superior, University of Zaragoza Spain, June 18-21 2007. Taylor & Francis Group, London, ISBN 978-0-415-44056-1, 95-114, 2007.

Šimůnek, J., and M. Th. van Genuchten, Modeling nonequilibrium flow and transport with HYDRUS, Vadose Zone Journal, doi:10.2136/VZJ2007.0074, Special Issue “Vadose Zone Modeling”, 7(2), 782-797, 2008.

Šimůnek, J., M. Th. van Genuchten, and M. Šejna, Development and applications of the HYDRUS and STANMOD software packages and related codes, Vadose Zone J 7(2), 587-600, 2008.

Šimůnek, J., M. Th. van Genuchten, and M. Šejna, The HYDRUS Software Package for Simulating Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Technical Manual, Version 2.0, PC Progress, Prague, Czech Republic, pp. 258, 2011.

Toride, N., F. J. Leij, and M. Th. van Genuchten, A comprehensive set of analytical solutions for nonequilibrium solute transport with first-order decay and zero-order production, Water Resour. Res., 29(7), 2167-2182, 1993.

van Genuchten, M. Th., A closed form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., 44, 892 898, 1980.

van Genuchten, M. Th., Non-equilibrium transport parameters from miscible displacement experiments, Research Report No. 119, U.S. Salinity Laboratory, Riverside, CA, 1981.

van Genuchten, M. Th., and F. N. Dalton, Models for simulating salt movement in aggregated field soils, Geoderma, 38, 165-183, 1986.

van Genuchten, M. Th., and J. Šimůnek, Integrated modeling of vadose zone flow and transport processes, Proc. Unsaturated Zone Modelling: Progress, Challenges and Applications, Eds. R. A. Feddes, G. H. de Rooij, and J. C. van Dam, Wageningen UR Frontis Series, Vol. 6, Chapter 2, pp. 37- 69, x-xi, Kluwer Academic Publishers, Dordrecht, The Netherlands, 2004.