Numerical methods usually subdivide the time and spatial coordinates into smaller pieces, such as finite differences, finite elements, and/or finite volumes, and reformulate the continuous form of governing partial differential equations in terms of a system of algebraic equations. In order to obtain solutions at certain times, numerical methods generally require intermediate simulations (time-stepping) between the initial condition and the points in time for which the solution is needed. HYDRUS models use the method of Finite Differences to integrate the governing equations (the Richards equation and the convection-dispersion equation) in time and the method of Finite Elements to solve the governing equations in space.
The Finite Element Mesh (FE-Mesh) is constructed by dividing the flow region for two-dimensional problems into Quadrilateral and/or Triangular Elements or for three-dimensional problems into Tetrahedral, Hexahedral, and/or Triangular Prismatic Elements whose shapes are defined by the coordinates of the nodes that form the element corners. The computational programs automatically subdivide the quadrilaterals into triangles (or hexahedrals and triangular prisms into tetrahedrals), which are then treated as subelements.
While Simple Geometries (see Geometry Types) are discretized using a Structured Finite Element Mesh (i.e., quadrilaterals and hexahedrals), General Geometries use an Unstructured Finite Element Mesh (i.e., triangles, tetrahedrals, and triangular prisms).
1. An examples of a Structured FE-Mesh for Simple Rectangular Geometries (discretized using quadrilateral elements):
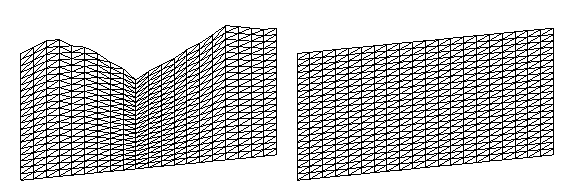
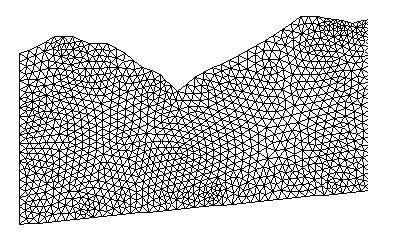
2. An example of a Unstructured FE-Mesh for a General Two-Dimensional Geometry (discretized using triangular elements):
3. An example of a Structured FE-Mesh for a Simple Hexahedral Three-Dimensional Geometry (discretized using hexahedral elements; displayed as divided into tetrahedrals):

4. An example of an Unstructured FE-Mesh for a Three-Dimensional Layered Geometry (discretized using triangular prisms):

More information about the 3D-Layered Geometries.
5. An examples of an Unstructured FE-Mesh for a Three-Dimensional General Geometry (discretized using tetrahedrals) :

Back to HYDRUS Step by Step.