Inverse Solution

The Inverse Solution dialog window (below) appears only when the Inverse Problem in the Main Processes dialog window is selected. Users select which parameters (the soil hydraulic, solute transport and reaction, and/or heat transport parameters) are to be optimized (Estimate …) from the specified experimental data.

HYDRUS implement a Marquardt-Levenberg type parameter estimation technique [Šimůnek and Hopmans, 2002] for inverse estimation of soil hydraulic (Hopmans et al., 2002) and/or solute transport and reaction [Šimůnek et al., 2002] parameters from measured transient or steady-state flow and/or transport data.

One also selects the method of Weighting of Inversion Data in the objective function. Users can choose between no weighting, weighting by mean ratios, or weighting by standard deviations. When no weighting is selected, one needs to supply weights for particular data points in the Data for Inverse Solution dialog window. When weighting by mean ratio or weighting by standard deviation is selected, then the code calculates either the means or the standard deviations of the different data sets (e.g., water contents, pressure heads, concentrations, …) and adjusts the weights proportionally. These internal weights can still be multiplied by weights from the Data for Inverse Solution dialog window.

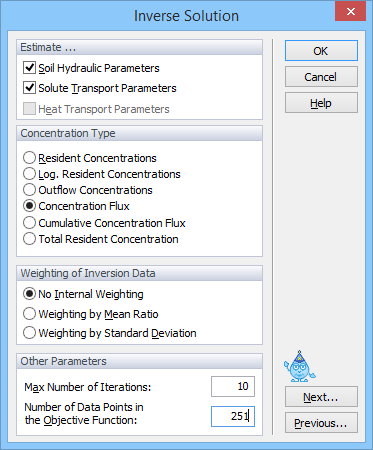
The objective function for the inverse estimation of solute transport parameter can be defined using different types of concentrations. Available Concentration Types are:

a) the resident concentration in the liquid phase,

b) a log-transformation of the resident concentration in the liquid phase,

c) the outflow (flux) concentration,

d) the solute concentration flux,

e) the cumulative concentration (solute) flux, and

f) the total resident concentration. The total resident concentration includes concentrations in the sorbed and nonequilibrium phases.

The maximum number of iterations for the inverse solution is also specified in this dialog window. If one selects zero number of iterations then only the direct simulation is carried out. However, users can still enter measured data, in which case the code compares results of the direct simulation with the measured data.

HYDRUS allows users to optimize up to 15 parameters (NPaD is the maximum allowed number of optimized parameters). We, however, do not recommend optimizing that many parameters simultaneously. Unsaturated flow problems are inherently ill-posed, and thus not too many parameters can be successfully optimized simultaneously. When more parameters are optimized, the problem often becomes nonunique. The problems of unsaturated flow are different than those of the saturated flow where it is common to optimize many more parameters simultaneously. For details see Šimůnek and Hopmans [2002], Hopmans et al. [2002] and Šimůnek et al. [2002].

Hopmans, J. W., J. Šimůnek, N. Romano, and W. Durner, Inverse Modeling of Transient Water Flow, In: Methods of Soil Analysis, Part 1, Physical Methods, Chapter 3.6.2, Eds. J. H. Dane and G. C. Topp, Third edition, SSSA, Madison, WI, 963-1008, 2002.

Šimůnek, J., and J. W. Hopmans, Parameter Optimization and Nonlinear Fitting, In: Methods of Soil Analysis, Part 1, Physical Methods, Chapter 1.7, Eds. J. H. Dane and G. C. Topp, Third edition, SSSA, Madison, WI, 139-157, 2002.

Šimůnek, J., D. Jacques, J. W. Hopmans, M. Inoue, M. Flury, and M. Th. van Genuchten, Solute Transport During Variably-Saturated Flow - Inverse Methods, In: Methods of Soil Analysis, Part 1, Physical Methods, Chapter 6.6, Eds. J. H. Dane and G. C. Topp, Third edition, SSSA, Madison, WI, 1435-1449, 2002.