Colloid, Virus and Bacteria Transport

Virus, colloid, and bacteria transport and fate models commonly employ a modified form of the advection-dispersion equation. In this work, we define the mass balance equation for these applications as:

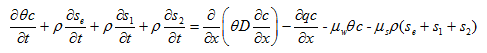
where c is the (colloid, virus, bacteria) concentration in the aqueous phase [ML-3], s is the solid phase (colloid, virus, bacteria) concentration [MM-1], subscripts e, 1, and 2 represent equilibrium and two kinetic sorption sites, respectively, and μw and μs represent inactivation and degradation processes in the liquid and solid phases, respectively.

While sorption to equilibrium sites can be described using standard equilibrium approaches, mass transfer between the aqueous and both solid kinetic phases can be described as (note that we dropped subscripts 1 and 2):

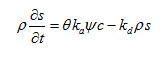
where ka is the first-order deposition (attachment) coefficient [T-1], kd is the first-order entrainment (detachment) coefficient [T-1], and ψ is a dimensionless colloid retention function [-]. The attachment and detachment coefficients have been found to strongly depend upon water content, with attachment significantly increasing as the water content decreases.

To simulate reductions in the attachment coefficient due to filling of favorable sorption sites, ψ is sometimes assumed to decrease with increasing colloid mass retention. A Langmuirian dynamics equation [Adamczyk et al., 1994] has been proposed for ψ to describe this blocking phenomenon as:

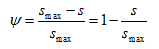
in which smax is the maximum solid phase concentration (MM-1). Conversely, enhanced colloid retention during porous medium ripening can theoretically be described using a functional form of ψs that increases with increasing mass of retained colloids:

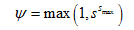
Johnson and Elimelech [1995] proposed a random sequential adsorption model to describe blocking of the sorption sites:

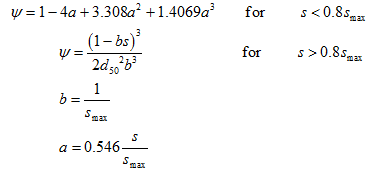
Finally, Bradford et al. [2003] hypothesized that the influence of straining and attachment mechanisms on colloid retention can be separated into two distinct components. They suggested the following depth dependent blocking coefficient for the straining process:

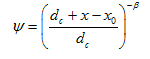
where dc is the diameter of the sand grains [L], x0 is the coordinate of the location where the straining process starts [L] (the surface of the soil profile, or the interface between soil layers), and β is an empirical factor (with an optimal value of 0.43 [Bradford et al., 2003]) [-].

The attachment coefficient can generally be calculated using filtration theory [Logan et al., 1995], a quasi-empirical formulation in terms of the median grain diameter of the porous medium (often termed the collector), the pore-water velocity, and collector and collision (or sticking) efficiencies accounting for colloid removal due to diffusion, interception and gravitational sedimentation [Rajagopalan and Tien, 1976; Logan et al., 1995):

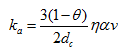
where α is the sticking efficiency (ratio of the rate of particles that stick to a collector to the rate at which they strike the collector) [-], v is the pore-water velocity [LT-1], and η is the single-collector efficiency [-]: 

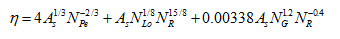
where the first, second, and third terms represent removal by diffusion, interception, and gravitational sedimentation, respectively, and where NPe is the Peclet number [-], NR is the interception number [-], NG is the gravitation number [-], NLo is the contribution of particle London-van der Walls attractive forces to particle removal [-], and As is a correction factor [-] as follows:

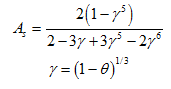
The dimensionless Peclet number is calculated as follows:

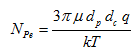
where μ is the fluid viscosity (= 0.00093 Pa s) [ML-1T-1], dp is the diameter of the particle (e.g., virus, bacteria) (= 0.95 μm = 0.95*10-6 m) [L], q is the Darcy’s flux [LT-1], k is the Boltzman constant (= 1.38048*10-23 J/K) [M L2 T-2 K-1], and T is the temperature (= 298 K) [K].

The interception number, NR, the gravitation number, NG, and the number representing London-van der Walls attractive forces, NLo, are calculated as:

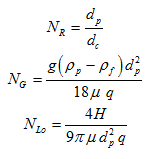
where H is the Hamaker constant (= 1*10-20 J) [ML2T-2], g is gravitational acceleration (= 9.81 m s-2) [LT-2], ρp is the bacterial density (= 1080 kg m-3) [ML-3], and ρf is the fluid density (= 998 kg m-3) [ML-3].

The model described above can be used in many different ways. One can for example assume that the soil has two sorption sites, s1 and s2, each having their own attachment and detachment constants. This model has been used to describe virus transport in sand dunes by Schijven and Šimunek [2002]. Sorption sites s1 and s2 can be used to describe straining and attachment, respectively, as was done by Bradford et al. [2002, 2003, 2004]. One can also assume that one sorption site represents sorption to the solid phase, while the other the removal of particles by their attachment to the air-water interface.