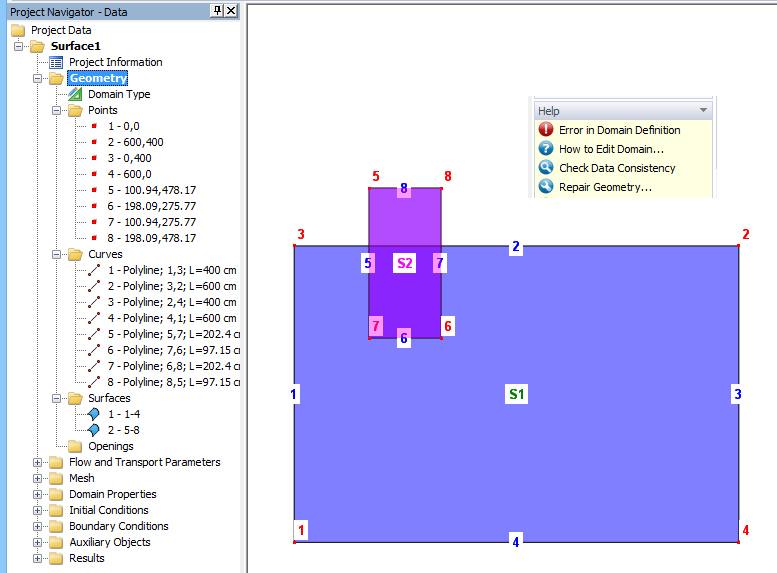
Objective: Create Surface No.2, which will partially covers bigger surface No.1.

Table of the definition objects (is not part of the Hydrus program).

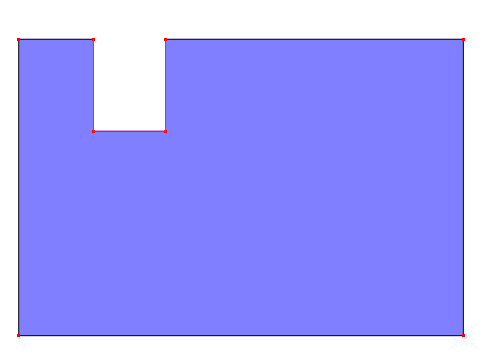
Goal: The two Surfaces shown above should not overlap. One should edit the boundary of Surface S1 so that Surface S2 defines it. Surface S2 does not overlap Surface S1, but it is inserted into the pocket of Surface S1, and the common boundary defines both Surfaces.

Procedure:

Because the common boundary of Surface S1 and newly created Surface S2 does not exist, an algorithm that permanently checks the correctness of geometry detects a topological error. See red Exclamation at the bottom of the Edit bar.

One can use the command "Repair Geometry ..." at the bottom of the Edit bar or edit the geometry manually.

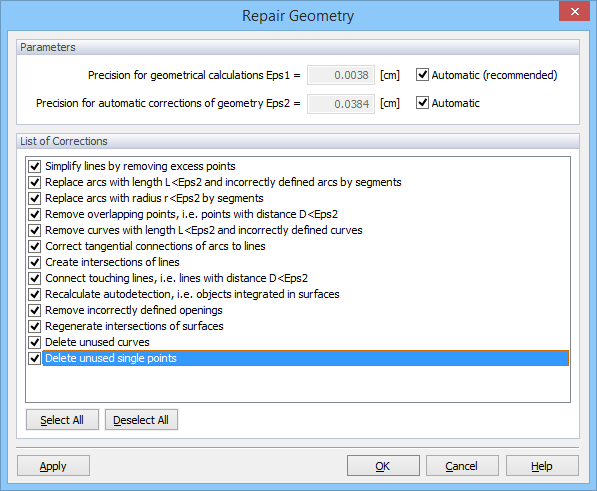
After confirming the List of Corrections in the Repair Geometry dialog window, the program automatically divides the lines that intersected into individual segments:

This automatic process creates intersection points 9 and 10 and splits the line between points 2 and 3 (originally line 2) into three new segments 2, 9, and 10 (similarly, it also splits lines 5 and 7 of Surface S2 into segments 5 and 11, and 7 and 12, respectively). The algorithm also redefines both Surfaces using these new segments instead of original lines 2, 5, and 7. However, Surface S1 is still defined using a large rectangle, even though with a larger number of definition curves.

Now we have two options:

1st approach: We can edit the list of boundary curves (i.e., replace line 9 with lines 11, 6, and 7) in the Edit Surface dialog window, which can be invoked by double-clicking on Surface S1.

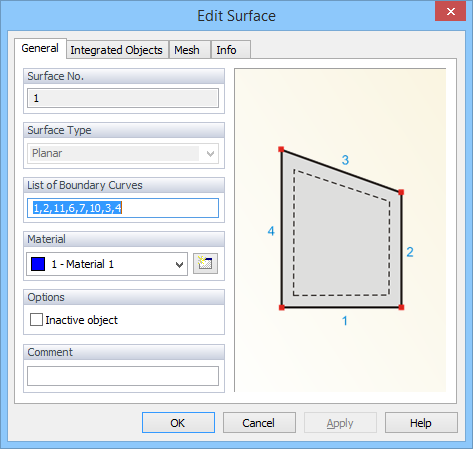
e.g. replaced line 9 with lines 11,6 and 7.

:

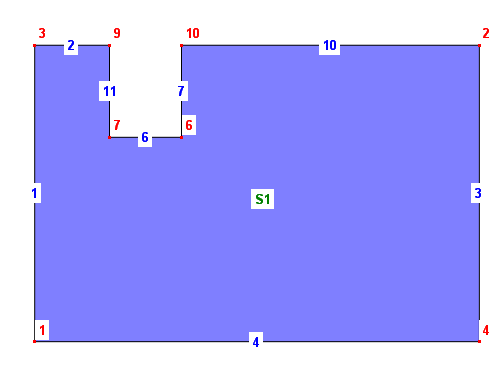
2nd approach: We can delete Surface S1 and create a new Surface using new boundary curves:

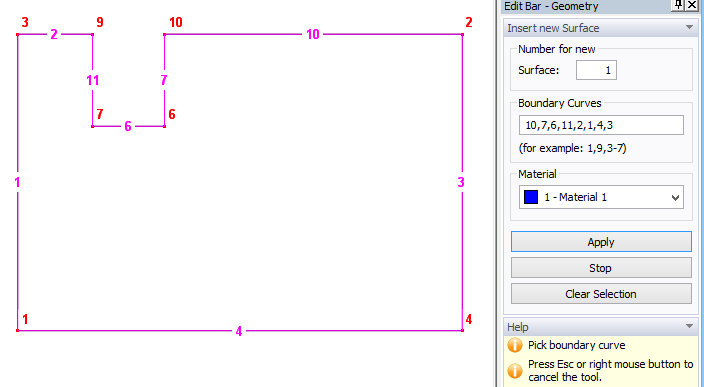
Line 9, formed by points 9 and 10, is no longer a boundary curve of either Surface and it can be deleted (it is not needed). Surface S2 is now inserted into the cutout of Surface S1, and common boundary curves 11, 6, and  7 are parts of the definition of both surfaces. Geometry is now correctly defined.

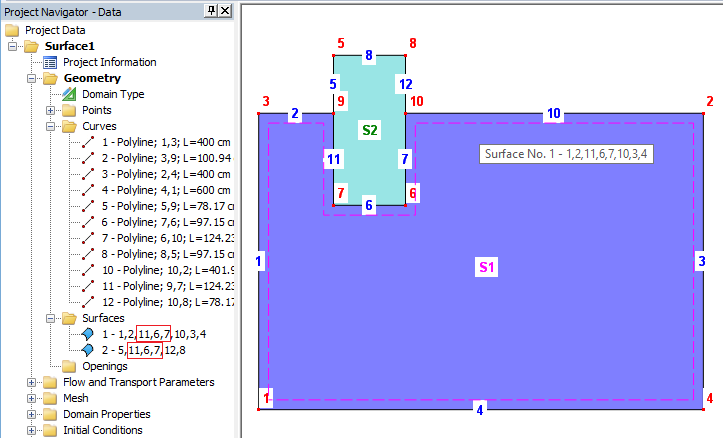
Conclusion: The definitions of both surfaces has been corrected by having both Surfaces to share common boundary curves (lines 11, 6, and 7). Surface S2 only looks like if it partially covers Surface S1.