In the Soil Hydraulic Model dialog window users select the Hydraulic Model to be used to describe the soil hydraulic properties, and specify whether or not Hysteresis is to be considered during the calculations.
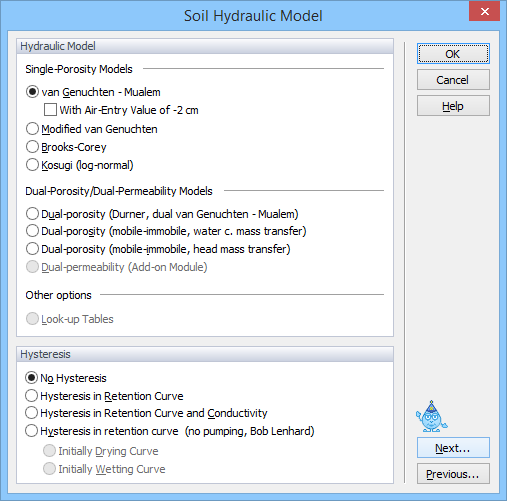
The Soil Hydraulic Model dialog window.
The code allows users to select six types of models for the soil hydraulic properties: a) the van Genuchten-Mualem model [van Genuchten, 1980], b) the van Genuchten-Mualem model with an air-entry value of -2 cm, c) the modified van Genuchten type equations [Vogel and Cislerova, 1988], d) the equations of Brooks and Corey [1964], e) the lognormal distribution model of Kosugi [1996], and f) a dual-porosity model [Durner, 1994]. Additionally, user can select two dual-porosity nonequilibrium flow models with mass transfer between the mobile and immobile zones assumed to be proportional to either g) the water content or h) the pressure head [Šimůnek et al., 2003]. For a detailed description of these models, see the technical manual of HYDRUS. Two other approaches (a dual-permeability model and look-up tables) are not available in the current version of HYDRUS.
Hysteresis:
When the van Genuchten model is used, either a) a non-hysteretic description (No Hysteresis), b) a hysteretic description only in the retention curve (Hysteresis in Retention Curve), or c) hysteretic descriptions in both the retention curve and the hydraulic conductivity curve (Hysteresis in Retention Curve and Conductivity) can be used. When hysteresis in the soil hydraulic properties is assumed, users must specify whether the initial condition is associated with the main wetting (Initially Wetting Curve) or main drying (Initially Drying Curve) retention curve. The HYDRUS code incorporates hysteresis by using the empirical model introduced by Scott et al. [1983]. This model was also employed by Kool and Parker [1987], who modified the formulation to account for air entrapment. While relatively simple to implement, the above model has been found to suffer sometimes from a so-called pumping effect, in which the hysteresis loops can move to physically unrealistic parts of the retention function. As an alternative, we also incorporated in HYDRUS the hysteresis model of Lenhard et al. [1991] and Lenhard and Parker [1992] that eliminates pumping by keeping track of historical reversal points (Hysteresis in Retention Curve, no pumping, Bob Lenhard).