Stochastic Distribution Parameters

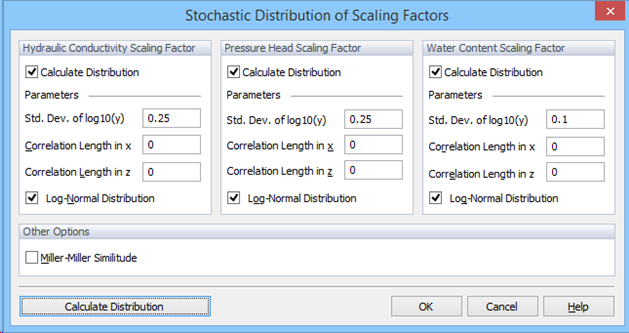
This option allows users to generate stochastically distributed scaling factors. Scaling factors for the pressure head, water content and hydraulic conductivity can either be completely independent of each other, or can be constrained by Miller-Miller similitude.

One can select either a normal or lognormal distribution for the scaling factors.

Spatial correlation can be accommodated using correlation lengths in both directions.

Parameters for generating scaling factors are specified in the Stochastic Parameters dialog window.

Procedures for generating autocorrelated or uncorrelated scaling factor fields have been described in detail by Freeze [1980] and El-Kadi [1986]. We used the original algorithm given by Mejia and Rodriguez-Iturbe [1974]. The residuals eij from a stochastic process N[0, 1; λY], in which the subscripts i=1,2,…I; j=1,2,…J denote the grid for the two-dimensional field of values to be generated, were taken as

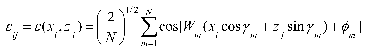
where xi and zi are horizontal and vertical directions of the two-dimensional field. For N>50, γm and ϕm are chosen from a uniform distribution over the range 0-2π, while Wm is given by

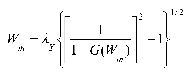
where G(Wm) is chosen from a uniform distribution over the range 0-1.

The input parameters for generating a two-dimensional log-normally distributed variable are the mean (μy) and standard deviation (σY) of the population, and the autocorrelation parameter λY. The values of my and σY are calculated using the following equations [Warrick and Nielsen, 1980]

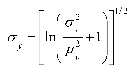
and

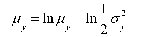
where μy and σY are the mean and the standard deviation, respectively, of the log-normally distributed variable before transformation.