Tensors of Anisotropy

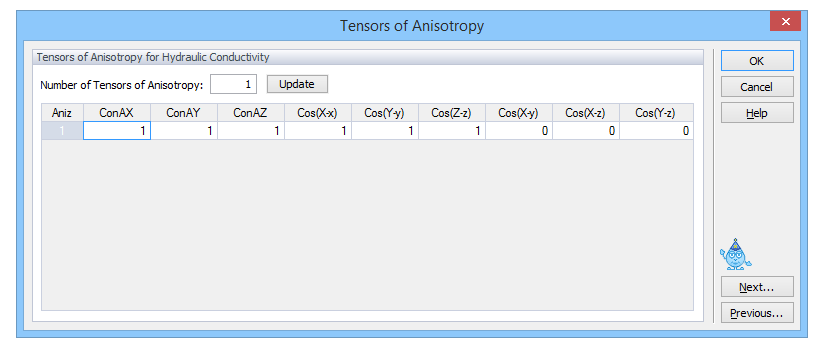
For two-dimensional problems users may need to specify the principal components K1A and K2A of the anisotropy tensor, together with the angle ùa  between the principal direction of K1A  and the x axis of the global coordinate system for each element. This has been simplified for three-dimensional problems where user can specify one or more Tensors of Anisotropy, which may be assigned to different parts of the transport domain. The anisotropy tensor is defined by three principal components, K1A  (ConAX), K2A  (ConAY), and K3A (ConAZ), and six coefficients aij that represent the cosine of angles between the ith principal direction of the tensor KA and the j-axis of the global coordinate system (i.e., Cos(X-x), Cos(Y-y), Cos(Z-z), Cos(X-y), Cos(X-z), Cos(Y-z)).