Water Flow
Dual-porosity models assume that water flow is restricted to the fractures (or inter-aggregate pores and macropores), and that water in the matrix (intra-aggregate pores or the rock matrix) does not move at all. These models assume that the matrix, consisting of immobile water pockets, can exchange, retain, and store water, but does not permit convective flow. This conceptualization leads to two-region, dual-porosity type flow and transport models [Philip, 1968; van Genuchten and Wierenga, 1976] that partition the liquid phase into mobile (flowing, inter-aggregate), θm, and immobile (stagnant, intra-aggregate), θim, regions:
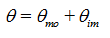
with some exchange of water and/or solutes possible between the two regions, usually calculated by means of a first-order rate equation. We will use here the subscript m to represent fractures, inter-aggregate pores, or macropores, and the subscript im to represent the soil matrix, intra-aggregate pores, or the rock matrix.
The dual-porosity formulation for water flow as used in HYDRUS is based on a mixed formulation, which uses Richards equation to describe water flow in the fractures (macropores), and a simple mass balance equation to describe moisture dynamics in the matrix as follows [Šimůnek et al., 2003]:
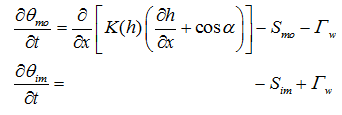
where Sm and Sim (Sim is assumed to be zero in the current HYDRUS version) are sink terms for both regions, and Γw is the transfer rate for water from the inter- to the intra-aggregate pores.
The mass transfer rate, Γw, for water between the fracture and matrix regions in several dual-porosity studies (e.g. Phillip [1968]; Šimůnek et al. [2003]) has been assumed to be proportional to the difference in effective saturations of the two regions using the first-order rate equation:
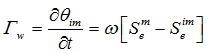
where θim is the matrix water content, ω is a first-order rate coefficient (T-1), and Sem and Seim are effective fluid saturations of the mobile (fracture) and immobile (matrix) regions, respectively. Equation above assumes that the mass transfer rate is proportional to the difference in effective water contents, rather than pressure heads [Gerke and van Genuchten, 1993b], which should provide a more realistic description of the exchange rate between the fracture and matrix regions. An inherent assumption is that the water retention properties of the matrix and the fracture domains are identical. For this reason, equation above must be used with some caution and probably only for dual-porosity models. The approach has nevertheless been used successfully in multiple studies (e.g., Köhne et al. [2004, 2005]).
An important advantage of the equation above is the fact that the dual-porosity model based on this mass transfer equation requires significantly fewer parameters since one does not need to know the retention function for the matrix region explicitly, but only its residual and saturated water contents. Coupling the equation above with a dual-porosity nonequilibrium flow model leads to the usual soil hydraulic parameters needed for the equilibrium model, two additional parameters characterizing the matrix region (i.e. its residual, θrim, and saturated, θsim, water contents), and the first-order mass transfer coefficient ω. By additionally assuming that the residual water content of the fracture region is equal to zero (and hence that residual water is present only in the immobile region), one could further decrease the number of model parameters.
When the rate of exchange of water between the fracture and matrix regions is assumed to be proportional to the difference in pressure heads between the two pore regions [Gerke and van Genuchten, 1993a], the coupling term, Γw, becomes:
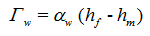
in which αw is a first-order mass transfer coefficient [L-1T-1]. Since pressure heads are now needed for both regions, this approach requires retention curves for both pore regions. For porous media with well-defined geometries, the first-order mass transfer coefficient, αw, can be defined as follows [Gerke and van Genuchten, 1993b]:
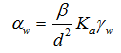
where d is an effective ‘diffusion’ pathlength (i.e. half the aggregate width or half the fracture spacing) [L], β is a shape factor that depends on the geometry [-], and γw is a scaling factor (=0.4) obtained by matching the results of the first-order approach at the half-time level of the cumulative infiltration curve to the numerical solution of the horizontal infiltration equation (Gerke and van Genuchten, 1993b). Gerke and van Genuchten [1996] evaluated the effective hydraulic conductivity Ka [LT-1] of the fracture-matrix interface using a simple arithmetic average involving both hf and hm as follows
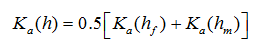
The use of these equations implies that the medium contains geometrically well-defined rectangular or other types of macropores or fractures (e.g. Edwards et al. [1979], van Genuchten and Dalton [1986], and Gerke and van Genuchten [1996]). While geometrically based models are conceptually attractive, they may be too difficult to use for field applications, partly because structured soils and rocks usually contain mixtures of aggregates and matrix blocks of various sizes and shapes, but also because the parameters may not be identifiable. Hence, rather than using this equation directly, one could also lump β, d, and γw into one effective hydraulic conductivity Ka* of the fracture-matrix interface to give
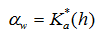
in which case Ka* can be used as a calibration parameter (this variable is an input parameter to HYDRUS).
The concept of two-region, dual-porosity type solute transport was implemented already in earlier versions (1.0 and 2.0) of HYDRUS-2D to permit consideration of physical nonequilibrium transport. While the physical nonequilibrium transport model in the earlier versions was combined only with uniform water flow (1), version 1.0 of HYDRUS (2D/3D) was expanded to also consider the dual-porosity water flow model with a transient immobile water content.
See also Dual-Permeability Models