While dual-porosity models assume that water in the matrix is stagnant, dual-permeability models allow for water flow in the matrix as well. The approach of Gerke and van Genuchten [1993a, 1996] who applied Richards equations to each of two pore regions is implemented in HYDRUS. The flow equations for the macropore or fracture (subscript f) and matrix (subscript m) pore systems in this approach are given by:
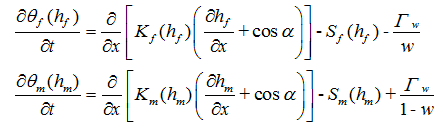
respectively, where w is the ratio of the volumes of the macropore or fracture domain and the total soil system [-], subscripts f and m refer to the fracture and matrix domains, θ is the volumetric water content [L3L-3], h is the pressure head [L], S is a sink term [T-1], xi (i=1,2) are the spatial coordinates [L], t is time [T], Γw is the transfer rate for water from the inter- to the intra-aggregate pores, KijA are components of a dimensionless anisotropy tensor KA, and K is the unsaturated hydraulic conductivity function [LT-1]. Note that the water contents θf and θm have different meanings than for dual-porosity models where they represented water contents of the total pore space (i.e., θ = θmo + θim), while here they refer to water contents of the two separate (fracture or matrix) pore domains such that θ = wθf + (1-w)θm =θF + θM, where θM and θF are absolute water contents in the matrix and macropore (fracture) regions, respectively).
Solutions of the Richards equation require knowledge of the unsaturated soil hydraulic functions made up of the soil water retention curve, θ(h), which describes the relationship between the water content θ and the pressure head h, and the unsaturated hydraulic conductivity function, K(h), which defines the hydraulic conductivity K as a function of h or θ. The dual-permeability approach, as developed by Gerke and van Genuchten [1993a], is relatively complicated in that the model requires characterization of water retention and hydraulic conductivity functions (potentially of different form) for both pore regions, as well as a hydraulic conductivity function of the fracture-matrix interface.
The rate of exchange of water between the fracture and matrix regions, Γw, is usually assumed to be proportional to the difference in pressure heads between the two pore regions [Gerke and van Genuchten, 1993a]:
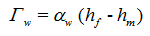
in which Γw is a first-order mass transfer coefficient [L-1T-1]. Since pressure heads are now needed for both regions, this approach requires retention curves for both pore regions. For porous media with well-defined geometries, the first-order mass transfer coefficient, Γw, can be defined as follows [Gerke and van Genuchten, 1993b]:
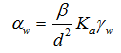
where d is an effective ‘diffusion’ pathlength (i.e., half the aggregate width or half the fracture spacing) [L], β is a shape factor that depends on the geometry [-], and γw is a scaling factor (=0.4) obtained by matching the results of the first-order approach at the half-time level of the cumulative infiltration curve to the numerical solution of the horizontal infiltration equation [Gerke and van Genuchten, 1993b]. The value of β varies with the geometry assumed for the aggregates [van Genuchten and Dalton, 1986]; it is 3 for rectangular slabs. Gerke and van Genuchten [1996] suggested a method for deriving values of the shape factor β for non-idealized geometries or mixtures of shapes in order to obtain a more general 'macroscopic' approach. Gerke and van Genuchten [1996] evaluated the effective hydraulic conductivity Ka [LT-1] of the fracture-matrix interface using a simple arithmetic average involving both hf and hm as follows
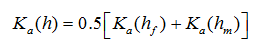
The use of this equation implies that the medium contains geometrically well-defined rectangular or other types of macropores or fractures (e.g., Edwards et al. [1979], van Genuchten and Dalton [1986], and Gerke and van Genuchten [1996]). While geometrically based models are conceptually attractive, they may be too difficult to use for field applications, partly because structured soils and rocks usually contain mixtures of aggregates and matrix blocks of various sizes and shapes, but also because the parameters may not be identifiable.
The dual-permeability formulation for solute transport is based on advection-dispersion type equations for transport in both the fracture and matrix regions as follows [Gerke and van Genuchten, 1993a,b]:
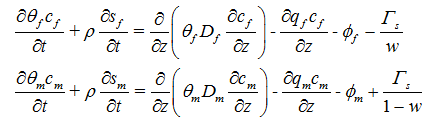
where subscripts f and m again refer to the fracture and matrix domains, c and s are solute concentrations in the liquid [ML-3] and solid [MM-1] phases, respectively; q is the volumetric flux density [LT-1], ρ is the soil bulk density [ML-3], Dij is the dispersion coefficient tensor [L2T-1] for the liquid phase, Γs is the mass transfer term for solute exchange between the fracture and matrix domains [ML-3T-1], and ϕ represents the sink/source term, accounting for first-order degradation and zero-order production processes, as well as root solute uptake. The first equation above describes solute transport in the fracture domain, the second equation transport in the matrix domain. Equation above assume complete advective-dispersive transport descriptions for both the fractures and the matrix.
Similarly as in the standard solute transport model of HYDRUS (2D/3D), the solute transport model in the dual-permeability module can be linked with the chemical nonequilibrium two-site sorption model or the physical nonequilibrium dual-porosity (mobile-immobile water) model. For governing equations of these two nonequilibrium models, see the technical manual of HYDRUS (2D/3D) [Šimůnek et al., 2011].
The advective-dispersive mass transfer between the fracture and matrix domains is traditionally described using the following form:
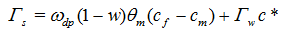
where Γs is the first-order solute mass transfer coefficient [T-1] accounting for physical rate process. c* is equal to cf for Γw>0 and cm for Γw<0. van Genuchten and Dalton [1986] and Gerke and van Genuchten [1996], among others, discussed possible expressions for the first-order solute mass transfer coefficient, αs [T-1], which can be defined as:
![]()
in which Da is an effective diffusion coefficient [L2T-1], which represents the diffusion properties of the fracture-matrix interface as well as other parameters.
See also the literature background beyond (and above used references) the Dual-Permeability Models.
See also Dual-Porosity Models.